Translate

martes, 16 de julio de 2013

MATEMATICA

TRIGONOMÉTRIA 
La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos". Deriva de los términos griegos τριγωνο trigōnotriángulo y μετρον metron medida.
En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.

Razones trigonométricas

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo  \alpha \, , correspondiente al vértice A, situado en el centro de la circunferencia.
  • El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa.
\sin \, \alpha = \frac{\overline{CB}}{\overline{AB}} = \frac{a}{c}
  • El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,
\cos\alpha = \frac{\overline{AC}}{\overline{AB}} = \frac{b}{c}
  • La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,
\tan\alpha = \frac{\overline{CB}}{\overline{AC}} = \frac{a}{b}


Razones trigonométricas inversas

  • La Cosecante: (abreviado como csc o cosec) es la razón inversa de seno, o también su inverso multiplicativo:
\csc \alpha = \frac{1}{\sin \; \alpha} = \frac{c}{a}
En el esquema su representación geométrica es:
\csc \alpha = \overline{AG}
  • La Secante: (abreviado como sec) es la razón inversa de coseno, o también su inverso multiplicativo:
\sec \alpha = \frac{1}{\cos \; \alpha} = \frac{c}{b}
En el esquema su representación geométrica es:
\sec \alpha = \overline{AD}
  • La Cotangente: (abreviado como cot o cta) es la razón inversa de la tangente, o también su inverso multiplicativo:
\cot \alpha = \frac{1}{\tan \alpha} = \frac{b}{a}
En el esquema su representación geométrica es:
\cot \alpha = \overline{GF}
Normalmente se emplean las relaciones trigonométricas seno, coseno y tangente, y salvo que haya un interés específico en hablar de ellos o las expresiones matemáticas se simplifiquen mucho, los términos cosecante, secante y cotangente no suelen utilizarse.
Publicado por en

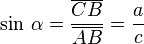
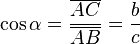
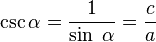
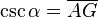
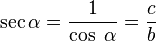
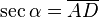
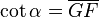
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)